スランプグラフから差枚数を自動算出するツール作成(後編)
前編に引き続きスランプグラフから差枚数を自動算出するツールをPythonで作っていきます。
前編で求めたグラフの位置からスランプグラフの差枚数を算出していきます。
2. スランプグラフから差枚数を求める
はじめに
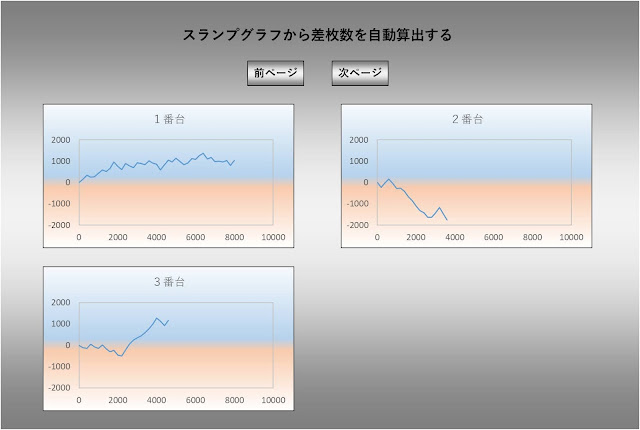
以下の画像から差枚数を算出していきますが、スランプグラフ内には差枚数算出に不必要なグラデーションが入っています。
人間の場合は、どれがグラフで、どれが不必要なグラデーションかを感覚的に判断できますが、コンピュータではどちらが必要なデータなのかはわかりません。
そこで、不必要なグラデーションを除去する処理を行います。
エッジ保存フィルタ(エッジ抽出フィルタ)と呼ばれる方法を採用しますが、これはその名の通り画像のエッジ(輪郭)だけを抽出する方法です。
言葉ではイメージしづらいと思うので、処理前後の画像を↓に貼っておきます。
画像全体からグラデーションが消えて、エッジ部分の線のみ残っています。
エッジ保存フィルタの中身の基本的な処理としては、画像の微分があげられます。
下図に示すように、微分の値は変化が急峻なところほど大きくなります。
これを画像にあてはめると、「変化が急峻なところ=画像のエッジ」、「変化が緩やかなところ=グラデーション部分」となるので、画像のエッジ部分だけを抽出することができます。
求めたエッジ部分を画像の端から探していけば、最初に見つかった点がグラフの最後の点がわかります。
最後に比例計算でピクセル数を差枚数に変換すれば差枚数算出完了です。
グラフの範囲は今回の場合±2000枚なので、全体として4000枚の範囲(2000×2枚)を計算しています。
画像のエッジ抽出
ここからは、Pythonでのコーディングに入ります。
まずは、画像のエッジ抽出を行います。
これまたテンプレートマッチングの時と同じく、1行だけです。
Canny法と呼ばれる方法を採用されているようですが、詳しいことは理解不足で説明できません。。
差枚数を求めたい画像は、「img_gray」に保存されているので、「img_gray」に対してエッジ抽出を行います。
# 差枚数を求めたい画像のエッジ抽出 img_bin = cv2.Canny(img_gray,128,200)
走査範囲の設定
続いて、グラフの最後の点を探していきますが、その前にグラフエリアの範囲を設定しておく必要があります。
(グラフの囲いの部分や、数字の部分はエッジ抽出で削除できないため。)
グラフエリアの範囲とは下図の範囲のことです。
使用するテンプレート画像を確認して、x, yそれぞれの最小値と最大値を設定します。
また、グラフの枠を検出してしまうと困るので、設定した範囲より「mergin」の値だけ内側を検索するようにします。
# グラフエリアの設定 x_min = 98 y_min = 97 x_max = 608 y_max = 320 # グラフエリアの大きさを計算 width = x_max - x_min height = y_max - y_min # グラフの枠を走査範囲から除くため数pixずらす mergin = 5
画像の走査
見つけたグラフの位置と、設定したグラフの範囲から、グラフの最後の点を探していきます。
1つのグラフあたり1点見つかった時点でループ処理を抜けるように「count」という変数を準備しています。
また、x方向のfor文を「for x in reversed(...」とすることで、グラフの右端から走査するようにしています。
# 見つかったエッジを入れる箱の準備
edge_x = []
edge_y = []
# 画像の走査
# for分でグラフを1つずつ処理
for pt in zip(*loc[::]):
# 1つのグラフで1個エッジが見つかれば良いので、ループを抜けるための変数を準備
count = 0
# x方向の範囲を右端から確認
for x in reversed(range(pt[1] + x_min, pt[1] + x_min + width - mergin)):
# y方向の範囲を上端から確認
for y in range(pt[0] + y_min, pt[0] + y_min + height - mergin):
# エッジ抽出された場所が見つかったら
if img_bin[y,x] == 255:
# x座標とy座標を記憶
edge_x.append(x)
edge_y.append(y)
# 場所がわかったので、ループから抜ける用のcountを更新
count = count + 1
# 1つのグラフで1箇所見つかったらループから抜ける
if count == 1:
break
# 1つのグラフで1箇所見つかったらループから抜ける
if count == 1:
break
# 見つかった座標を一つの配列にまとめる
edge = np.stack([edge_x, edge_y])
見つかった位置を確認してみましょう。
「edge」の中に記録した位置を1つずつ画像内に描画していきます。
# 見つけた位置に赤点を描画
for pt in zip(*edge[::]):
cv2.rectangle(img_rgb, (pt[0] - 1, pt[1] - 1), (pt[0] + 1, pt[1] + 1), (0,0,255), 5)
cv2.imwrite("D:\Test\edge.bmp",img_rgb)
結果は下図のようになりました。
問題なくグラフの最後の点(赤点部分)が取得できていますね。
差枚数の計算と表示
見つけた位置が問題なさそうなので、単位を差枚数に変換します。
変換に必要なのはy座標だけなので、「edge_y」に記録した位置ごとに計算していきます。
冒頭の比例計算の式にあてはめると、以下のようなコードになります。
# [pix]を[差枚数]に変換
# グラフのレンジ設定(±2000なら、2000と入力)
graph_range = 2000
for i in range(len(loc[1][:])):
edge_y[i] = ((loc[0][i] + (y_max + y_min) / 2) - edge_y[i]) * (graph_range * 2) / height
# 結果の出力
for i in range(len(edge_y[:])):
print(i + 1, "番台:", round(edge_y[i],0), "枚")
出力された結果がこちら。
見た目とはだいたいあってそうですね。
1 番台: 1049.0 枚 2 番台: -1749.0 枚 3 番台: 1193.0 枚
差枚数の計算と表示
今回は自作のグラフなので、元データとも比較してみます。
結果は、誤差数十枚となりました!!
このグラフだと人間なら数百枚ずれてもおかしくないと思うので、かなり優秀ではないでしょうか。
今回作成したコード
前回のグラフの位置を探すところから、差枚数を算出するまでのコードはこちらです。
# coding: UTF-8
import cv2
import numpy as np
# テンプレート画像の場所
Template_path = "D:\Test\Template.bmp"
# グラフを探したい画像の場所
Target_path = "D:\Test\Target.bmp"
# テンプレート画像の読み込み
template = cv2.imread(Template_path)
template_gray = cv2.cvtColor(template, cv2.COLOR_BGR2GRAY)
# グラフを探したい画像の読み込み
img_rgb = cv2.imread(Target_path)
img_gray = cv2.cvtColor(img_rgb, cv2.COLOR_BGR2GRAY)
# テンプレートマッチング実行
res = cv2.matchTemplate(img_gray,template_gray,cv2.TM_CCOEFF_NORMED)
# 閾値の設定。threshold=1だと全く同じ画像だけ認識する
threshold = 0.7
# 閾値以下のポイントを削除
loc = np.where( res >= threshold)
# # テンプレートマッチングで見つかった位置の表示
# for pt in zip(*loc[::]):
# print("x, y = ", pt[1], ", ", pt[0])
# print("----------------------------")
# 座標リストで近すぎる座標を削除
# Mergin[pix]の値より近い座標は削除する
Mergin = 10
index = []
for i in range(len(loc[1][:])):
count = 0
for j in range(len(loc[1][:])):
# Mergin[pix]の値より近い座標の番号をメモする
if abs(loc[1][:][i] - loc[1][:][j]) < Mergin and abs(loc[0][:][i] - loc[0][:][j]) < Mergin:
if count > 0:
index.append(j)
count = count + 1
# Mergin[pix]の値より近い座標の番号を削除する
loc = np.delete(loc, index, axis=1)
# テンプレートの画像サイズ確認
w, h = template_gray.shape[::-1]
# # テンプレートマッチングで見つかった位置の表示
# for pt in zip(*loc[::]):
# print("x, y = ", pt[1], ", ", pt[0])
# cv2.rectangle(img_rgb, (pt[1], pt[0]), (pt[1] + w, pt[0] + h), (0,0,255), 10)
cv2.imwrite("D:\Test\Template_Result.bmp",img_rgb)
# 差枚数を求めたい画像のエッジ抽出
img_bin = cv2.Canny(img_gray,128,200)
cv2.imwrite("D:\Test\Bin_Result.bmp",img_bin)
# グラフエリアの設定
x_min = 98
y_min = 97
x_max = 608
y_max = 320
# グラフエリアの大きさを計算
width = x_max - x_min
height = y_max - y_min
# グラフの枠を走査範囲から除くため数pixずらす
mergin = 5
# 見つかったエッジを入れる箱の準備
edge_x = []
edge_y = []
# 画像の走査
# for分でグラフを1つずつ処理
for pt in zip(*loc[::]):
# 1つのグラフで1個エッジが見つかれば良いので、ループを抜けるための変数を準備
count = 0
# x方向の範囲を右端から確認
for x in reversed(range(pt[1] + x_min, pt[1] + x_min + width - mergin)):
# y方向の範囲を上端から確認
for y in range(pt[0] + y_min, pt[0] + y_min + height - mergin):
# エッジ抽出された場所が見つかったら
if img_bin[y,x] == 255:
# x座標とy座標を記憶
edge_x.append(x)
edge_y.append(y)
# 場所がわかったので、ループから抜ける用のcountを更新
count = count + 1
# 1つのグラフで1箇所見つかったらループから抜ける
if count == 1:
break
# 1つのグラフで1箇所見つかったらループから抜ける
if count == 1:
break
# 見つかった座標を一つの配列にまとめる
edge = np.stack([edge_x, edge_y])
# 見つけた位置に赤点を描画
for pt in zip(*edge[::]):
cv2.rectangle(img_rgb, (pt[0] - 1, pt[1] - 1), (pt[0] + 1, pt[1] + 1), (0,0,255), 10)
cv2.imwrite("D:\Test\edge.bmp",img_rgb)
# [pix]を[差枚数]に変換
# グラフのレンジ設定(±2000なら、2000と入力)
graph_range = 2000
for i in range(len(loc[1][:])):
edge_y[i] = ((loc[0][i] + (y_max + y_min) / 2) - edge_y[i]) * (graph_range * 2) / height
# 結果の出力
for i in range(len(edge_y[:])):
print(i + 1, "番台:", round(edge_y[i],0), "枚")
# 見つかった位置を画像で表示
cv2.imshow("SlumpGraphCalcResult", img_rgb)
cv2.waitKey(0)
cv2.destroyAllWindows()
最低限の部分だけのコーディングですが、十分実用的なツールができたと思います。
にほんブログ村








コメント
コメントを投稿