スログラミング

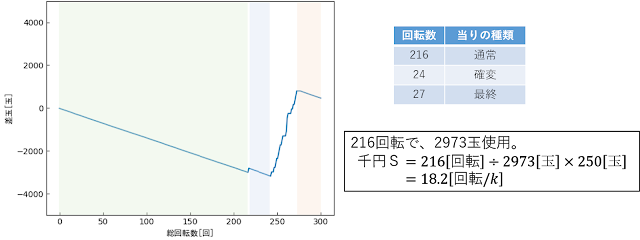
お世話になっております、スログラミングです。 今回はひさしぶりにpythonでプログラミングしようと思ってます。 遊技機の大型化。個人的にはエヴァとか牙狼みたいに動作するなら許せる派ですが、私の好みの話はどうでも良いので一旦おいておくとして、そういう機種でスランプグラフを撮ろうとすると、 こうなりません？ この状態だと、 スランプグラフから千円Ｓを計算 したりするときにちょっとめんどくさかったりします。 （そもそも目視でも見辛いですし。） そこで今回は、 斜めから撮影したスランプグラフを真っすぐに戻す方法 について説明したいと思います。 本日のアジェンダはこちら。 透視変換とは？ 透視変換のプログラミング 今回作成したコード まとめ 1. 透視変換とは？ 目次で答えが先バレしちゃってますが、斜めから撮影したスランプグラフを真っすぐに戻すには、 透視変換 を使います。 射影変換というのもあるらしいですが、違いはよくわかってません。 そこら辺の説明は頭の良い方にお任せするとして、斜めに撮った状態のまま千円Ｓを算出するとどうなってしまうかを考えてみましょう。 他にも方法はあるかもしれませんが、 基本的には1pixあたりの出玉数を計算することで、千円Ｓを算出 すると思います。 例えば、冒頭で貼り付けた画像の場合、グラフの左端は0~10000玉までのサイズが522pixなのに対して、右端は384pixとなっています。 この場合、1pixあたりの出玉数は、 ・左端：10000[玉] / 522[pix] = 19.16[玉/pix] ・右端：10000[玉] / 384[pix] = 26.04[玉/pix] となるので、 左端で求めた1pixあたりの出玉数を使って、右端の出玉数を算出したりするとおかしな値となってしまい ます。 （1pixあたり5玉ずつずれていく。） 左端の出玉数は左端で求めた1pixあたりの出玉数を使って、右端の出玉数は右端で求めた1pixあたりの出玉数を使う、とか

お世話になっております、スログラミングです。 ずっと「1kあたりの回転数」って言ってましたが、「 千円Ｓ(千円スタート) 」っていう便利な呼び方があるんですね。 勉強になります。 個人的に千円Ｓは、非等価店で等価ボーダーくらい回れば満足ですが、なるべくなら回る台を打ちたいですよね。 最近では、機種ごとに釘の見方を解説してくれる便利なサイトもありますが、私には釘を見分けるセンスがなかったようで諦めました。。。 ということで、タイトルにつながってきます。 スランプグラフを解析すれば千円Ｓわかるんじゃない？ ってことですね。 では、pythonでプログラミングしていきましょう。 ※シミュレーションに使う数値や結果はスログラミング調べということで鵜呑みにしないでください。 本日のアジェンダはこちら。 1. スランプグラフから千円Ｓを算出する方法 2. スランプグラフの準備 3. スランプグラフのデータ位置を取得 4. 取得したデータを解析 5. 今回作成したコード 6. 結果の確認 1. スランプグラフから千円Ｓを算出する方法 まずは、どのようにしてスランプグラフから千円Ｓを算出するかを考えていきます。 例えばこんな感じのスランプグラフがあったとして、当然右肩下がりの部分が通常時とわかります。 (色付けした３ヶ所) 後半２ヶ所(水色とピンク)の部分は、回転数が少なく回転ムラの影響が大きそうなので、 長いハマり(緑色)のところの差玉から千円Ｓを算出 するのが、一番簡単ですね。 今回の例だと、216回転回すのに2973玉使っているので、1玉当りの回転数は216/2973[回/玉]となります。 千円当たり250玉なので、千円Ｓ＝216/2973*250[回/k]で計算できますね。 とはいえ、これだとちょっともったいない気もします。 人力でざっくり計算するときはこれでも良いですが、せっかくプログラムを組んで計算するなら 水色やピンクの部分も含めて千円Ｓを計算したい ですよね。 ということで、今回はこんな感じで千円Ｓを計算したいと考えています。 1. スランプグラフからデータを抽出 2. スランプグラフから通常時の部分を抽出 3. 抽出した通常時部分から千円Ｓを算出 こうすることで、早い当りの時の通常時のデータ

お世話になっております、スログラミングです。 「 波理論 」。パチンコ・スロット好きな方なら一度は聞いたことがありますよね。 例えば、こんな感じで過去のスランプグラフから未来のスランプグラフを予想するオカルトです。 とはいえ、パチンコ・スロットが完全確率である限り 予想は不可能 なわけですが、楽しみ方の一つとして個人的には好きなオカルトです。 ※怪しい情報教材にはくれぐれもご注意ください。 では早速Pythonでコーディングしていきましょう。 今回のアジェンダはこちら。 1. 波理論とは？ 2. 波理論部分のコード 3. 今回作成したコード 4. 結果の確認 1. 波理論とは？ 冒頭でちらっと記載しましたが、もう少し具体的に波理論の中身を考えてみます。 おそらく波理論をやるときの頭の中はこうなっていると思います。 １．スランプグラフを見る ２．頭の中にある過去のスランプグラフと照合 ３．今のと似たスランプグラフをピックアップ ４．ピックアップしたスランプグラフをパターン分類 ５．頻出するパターンになると予想 ここまでの流れを元に、プログラミングを行うためのフローチャートを作成したものがこちら。 実戦データベースは、過去に作成した マイジャグのシミュレータ をちょっといじってcsv出力してます。 csvの中身は１列だけで、１回転ごとの差枚数をひたすら出力してます。 今回の評価方法は以下の形としています。 １．３０００Ｇ分のスランプグラフを作成 ２．その内、２０００Ｇ分のデータから波理論で残りの１０００Ｇの推移を予測 ３．機種はマイジャグ、設定は１ 想定としては、「軽く回されて判別やめされた設定１のマイジャグを１時間超くらいでさくっと出したい！」という感じです。 2. 波理論部分のコード ここから実際のコーディングを行っていきます。 (フローチャートの スランプグラフ作成 の部分はいつもと同じなので割愛。) 必要なデータの読み込み まずは、必要なデータを読み込んでいきます。 csvデータの読み込みは、numpy(今回使用)とpandasがありますが、numpyに入っている相互相関(corrcoef)を使いたいのでnumpyで読み込んでいます。 また、コメントに記載しましたが、以下のようにデ

突然ですが、ジャグラーで↓のスランプグラフの時、設定はいくつだと思いますか？ きっと大多数の方が「設定６」と答えるのではないでしょうか？ では、こちらはどうでしょう？ はい、「設定１」ですよね。 これってたぶん、我々スロッターの頭の中では過去に見てきたたくさんのスランプグラフが脳にインプットされていて、そこから今見たスランプグラフがどの記憶に似ているかで判断していると思います。 今回はこれをコンピュータにやらせてみたい！ ということで、スランプグラフから設定判別してくれるなんちゃってAIを作成したいと思います。 (あくまでも素人が思いつきで作ったようなレベルなので、緩い目でご覧ください。) 今回はマイジャグラーⅢを例に、スランプグラフの傾向から設定判別してみます。 はじめに 今回は以下の流れで実験を行います。 1. 判別したいスランプグラフを作成 2. 設定ごとのビッグデータ(スロッターの脳にあるたくさんのスランプグラフの記憶)を作成 3. 判別したいスランプグラフに似た傾向がビッグデータ内にどれくらいあるかを確認 4. 各設定のビッグデータ内で、近いデータがいっぱい見つかった設定が今回の設定！（のはず。） 当然「3. 判別したいスランプグラフに似た傾向がビッグデータ内にどれくらいあるかを確認」が最も大事になってきますが、今回は「相互相関」という手法を使って検証していきます。 どうやってスランプグラフの傾向を評価するか？(相互相関) 「相互相関」とは、ある2つのデータの類似度を評価する手法です。 例によってpythonでは↓の1行で計算してくれるわけですが、せっかくなので中身の計算のイメージだけでもつかんでおきたいと思います。 np.corrcoef(ビッグデータから1日分抜き出したデータ, 1日分のスランプグラフ)[0,1] 「相互相関」の中身の計算は、「内積」とほぼ同じなので、「内積」の計算について説明します。 「内積」は線形代数で勉強したあの「内積」で、以下の計算式で求められます。 ↑の式をcosθの式に直すと、↓のようになります。 この式が「相互相関」でやっていることとほぼ同じです。 ちょっと式を見てもわからないので、下図に例を計算してみました。 ベクトルだと考えると理解しにくいですが、スランプグラ

前編に引き続きスランプグラフから差枚数を自動算出するツールをPythonで作っていきます。 前編で求めたグラフの位置 からスランプグラフの差枚数を算出していきます。 2. スランプグラフから差枚数を求める はじめに 以下の画像から差枚数を算出していきますが、スランプグラフ内には差枚数算出に不必要なグラデーションが入っています。 人間の場合は、どれがグラフで、どれが不必要なグラデーションかを感覚的に判断できますが、コンピュータではどちらが必要なデータなのかはわかりません。 そこで、不必要なグラデーションを除去する処理を行います。 エッジ保存フィルタ(エッジ抽出フィルタ)と呼ばれる方法を採用しますが、これはその名の通り画像のエッジ(輪郭)だけを抽出する方法です。 言葉ではイメージしづらいと思うので、処理前後の画像を↓に貼っておきます。 画像全体からグラデーションが消えて、エッジ部分の線のみ残っています。 エッジ保存フィルタの中身の基本的な処理としては、画像の微分があげられます。 下図に示すように、微分の値は変化が急峻なところほど大きくなります。 これを画像にあてはめると、「変化が急峻なところ＝画像のエッジ」、「変化が緩やかなところ＝グラデーション部分」となるので、画像のエッジ部分だけを抽出することができます。 求めたエッジ部分を画像の端から探していけば、最初に見つかった点がグラフの最後の点がわかります。 最後に比例計算でピクセル数を差枚数に変換すれば差枚数算出完了です。 グラフの範囲は今回の場合±2000枚なので、全体として4000枚の範囲(2000×2枚)を計算しています。 画像のエッジ抽出 ここからは、Pythonでのコーディングに入ります。 まずは、画像のエッジ抽出を行います。 これまたテンプレートマッチングの時と同じく、1行だけです。 Canny法と呼ばれる方法を採用されているようですが、詳しいことは理解不足で説明できません。。 差枚数を求めたい画像は、「img_gray」に保存されているので、「img_gray」に対してエッジ抽出を行います。 # 差枚数を求めたい画像のエッジ抽出 img_bin = cv2.Canny(img_gray,128,200) 走査範囲の設定 続いて、グラフの最後の点を探してい