スランプグラフから千円S(千円スタート:パチンコの回転数)算出
お世話になっております、スログラミングです。
ずっと「1kあたりの回転数」って言ってましたが、「千円S(千円スタート)」っていう便利な呼び方があるんですね。
勉強になります。
個人的に千円Sは、非等価店で等価ボーダーくらい回れば満足ですが、なるべくなら回る台を打ちたいですよね。
最近では、機種ごとに釘の見方を解説してくれる便利なサイトもありますが、私には釘を見分けるセンスがなかったようで諦めました。。。
ということで、タイトルにつながってきます。
スランプグラフを解析すれば千円Sわかるんじゃない?ってことですね。
では、pythonでプログラミングしていきましょう。
※シミュレーションに使う数値や結果はスログラミング調べということで鵜呑みにしないでください。
本日のアジェンダはこちら。
1. スランプグラフから千円Sを算出する方法
まずは、どのようにしてスランプグラフから千円Sを算出するかを考えていきます。
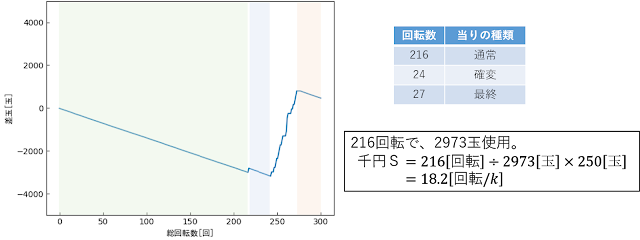
例えばこんな感じのスランプグラフがあったとして、当然右肩下がりの部分が通常時とわかります。
(色付けした3ヶ所)
後半2ヶ所(水色とピンク)の部分は、回転数が少なく回転ムラの影響が大きそうなので、長いハマり(緑色)のところの差玉から千円Sを算出するのが、一番簡単ですね。
今回の例だと、216回転回すのに2973玉使っているので、1玉当りの回転数は216/2973[回/玉]となります。
千円当たり250玉なので、千円S=216/2973*250[回/k]で計算できますね。
とはいえ、これだとちょっともったいない気もします。
人力でざっくり計算するときはこれでも良いですが、せっかくプログラムを組んで計算するなら水色やピンクの部分も含めて千円Sを計算したいですよね。
ということで、今回はこんな感じで千円Sを計算したいと考えています。
1. スランプグラフからデータを抽出
2. スランプグラフから通常時の部分を抽出
3. 抽出した通常時部分から千円Sを算出
こうすることで、早い当りの時の通常時のデータも無駄にすることなく、計算に活用できます。
2. スランプグラフの準備
実際のスランプグラフを使用すると、千円Sの答え合わせができないので、まずは解析用のスランプグラフを準備します。
ここは本題とは関係なので、興味のない方は次の項目に進んでください。
今回の千円S算出では、個人的に以下の点を懸念しています。
1. ショボ出玉に騙されないか?
最近は、初当りの出玉が数100発程度ですぐに通常時に落ちてしまう機種が増えてきています。
先ほどのスランプグラフだとこの部分ですね。
このショボ出玉分も通常時と判定してしまうと、千円Sが実際よりも良い値になってしまいます。
ということで、スランプグラフを作成する機種は、韋駄天ライト(3R通常で240玉)にしたいと思います。
2. 実機の回転ムラをどのように解析用スランプグラフに取り込むか?
これはどちらかというと、今まで作成したシミュレータの問題ですが、実際の機械では結構回転ムラがありますよね。
実際のスランプグラフは当然回転ムラが含まれたデータになっているので、今回のシミュレータでは回転ムラを考慮したコーディングを行わなければいけません。
・回転ムラの考慮方法
回転ムラの考慮に関して、具体的にはnumpyのrandom.normal関数を用いることで対応します。
ざっくりいうと、numpyのrandom.normal関数を用いることで正規分布に従った乱数を生成できます。
例えば、randomのrandint関数では、以下のヒストグラムのように全ての乱数が均等に出現します。
それに対して、numpyのrandom.normal関数のヒストグラムは以下のように、予め決めた値(今回は18)を基準に正規分布に従うように乱数が出現します。
使い方は、以下のように(基準にしたい値, どのくらいの幅を持たせるか)を指定するだけでOKです。
今回は、整数値が欲しかったので、round関数も併せて使用しています。
import numpy as np
rand = round(np.random.normal(千円S, 2),0)
3. スランプグラフのデータ位置を取得
ここから、千円S算出処理の内容に入っていきます。
・グラフ位置の特定
まずは、グラフの位置を特定していきます。
過去記事で使用したテンプレートマッチングを使います。
ターゲット画像(スランプグラフ)と、テンプレート画像はこんな画像を準備してます。
テンプレートマッチングで得られた座標リストから、類似度が最大の座標をグラフの位置と決定しています。
# ターゲット画像の準備
target = cv2.imread(r"D:\Test\slump.png")
target_gray = cv2.cvtColor(target, cv2.COLOR_BGR2GRAY)
cv2.imwrite(r"D:\Test\target_gray.png", target_gray)
# テンプレート画像の準備
template = cv2.imread(r"D:\Test\template.png")
template_gray = cv2.cvtColor(template, cv2.COLOR_BGR2GRAY)
cv2.imwrite(r"D:\Test\template_gray.png", template_gray)
# テンプレートマッチング
match = cv2.matchTemplate(target_gray, template_gray, cv2.TM_CCOEFF_NORMED)
# 類似度が最大値の場所をグラフの位置に決定
loc = np.unravel_index(np.argmax(match), match.shape)
・データ位置の抽出
続いてグラフの中のデータ位置を抽出します。
ざっくりいうと画像同士の引き算を行ってデータ位置だけを残します。
流れとしては、こんな感じです。
1. ターゲット画像と同じサイズの無地の画像を準備
2. マッチング位置にテンプレート画像を貼り付け
3. マッチング位置で画像同士を引き算
・モルフォロジ処理
基本的な流れは↑のでOKですが、今回は引き算の前にひと手間加えています。
例えば、以下のようにマッチング位置が少しずれてしまったとき、グラフの枠線が残ってしまい、後の解析の邪魔になってしまいます。
こんな時の解決策の一例として、モルフォロジ処理があります。
モルフォロジ処理の基本的な処理として、膨張(Dilation)と収縮(Erosion)があります。
例えば、"B"という文字にそれぞれの処理を行うと、下図のようになります。
名前の通り、膨張は太くなる、収縮は細くなる感じです。
つまり、多少マッチング位置がずれてもテンプレート画像を太らせてしまえば引き算したときに余計な部分を消せるという対処方法です。
※画像内では膨張と書きましたが、正確には縮小処理を行います。
(画像処理では白色の部分が膨張or収縮するので、黒色の枠画像のときは逆になる。)
pythonでは、以下のような形で使用します。
kernel(画像処理を行う際の窓の大き)と、iteratioins(処理の実行回数)を大きくするほど、処理後の画像が収縮(or膨張)します。
kernel = np.ones((5, 5), np.uint8)
img_erode = cv2.erode(img, kernel, iterations = 3)
ここで、元に戻ってデータ位置だけを残す部分の処理はこちら。
引き算の部分にnp.whereを使用しているのは、枠画像が黒だからです。
(黒=画素値0なので、0を引き算しても何も起こらない。)
# テンプレート画像をマッチングした位置に移動
# 無地の画像を作成して、そこにテンプレート画像を貼り付ける。
# OpenCVとPillowで画像の読み込みが異なるので、Image.openとcv2.imreadを使って何度も画像を読み込んでいる。
w_tgt, h_tgt = target_gray.shape
ImgMove = Image.new("RGB", (h_tgt, w_tgt), (0, 0, 0))
NumImg_pil = Image.open(r"D:\Test\template_gray.png")
ImgMove.paste(NumImg_pil, (loc[1], loc[0]))
ImgMove.save(r"D:\Test\template_move.bmp")
MoveImg = cv2.imread(r"D:\Test\template_move.bmp", 0)
# モルフォロジを行って微妙な位置ずれでも邪魔なピクセルを消せるようにする。
# 今回はグラフが黒線なのでErosion(収縮)を使う。グラフが白線の場合はDilation(膨張)を使う。
kernel = np.ones((5, 5), np.uint8)
DilImg = cv2.erode(MoveImg, kernel, iterations = 3)
cv2.imwrite(r"D:\Test\target_mor.png", DilImg)
# グラフの線が黒色なので、反転したうえで引き算
# これでグラフの中身だけが残る
SubImg = np.where(target_gray < DilImg, target_gray, 0)
cv2.imwrite(r"D:\Test\target_sub.png", SubImg)
処理後の画像は、このような感じになります。
枠部分の画像が消えて、グラフのデータ位置だけが残っていることがわかります。
・データの取得
ここから、処理後の画像を解析してスランプグラフのデータを取得していきます。
手法はいたってシンプルです。
上から下まで走査し、黒(画素値=0)以外の画素位置がデータの位置!となります。
これを画像の左から右まで実行すればOKです。
コードはこちら。
各列1pix見つかったらbreakで抜けることで、処理がかなり早くなります。
各列複数pix見つけてそれらの平均としても良いですが、絶対値にはあまり意味がないので個人的にはそこまでやらなくても良いと思います。
# 画像の走査
peakx = []
peaky = []
# テンプレート画像のサイズ
w, h = template_gray.shape[::-1]
# 画像の走査範囲の描画
cv2.rectangle(target, (loc[1], loc[0]), (loc[1] + w, loc[0] + h), (0, 0, 255), 2)
cv2.imwrite(r"D:\Test\target_match.png", target)
# ピーク位置(スランプグラフ)の検出
for i in range(loc[1], loc[1] + w):
for j in range(loc[0], loc[0] + h):
# ピーク位置(画素が白=255のところがグラフの位置)
if SubImg[j, i] != 0:
peakx.append(i)
peaky.append(j)
# X方向1pixごとに、Y方向のピークは1個見つかればOK
break
取得したデータをスランプグラフに描画したものがこちら。
水色が元のスランプグラフ、青色が取得したスランプグラフですが、元のスランプグラフがほとんど見えないくらい正確にデータ取得できていることがわかります。
4. 取得したデータを解析
ここまでくればあと一息です。
取得したデータを解析して千円Sを算出していきます。
・取得データの変換(pix->G数、pix->差玉)
まずは、取得したデータをG数と差玉に変換します。
以下の計算式で算出できます。
ちょっとごちゃごちゃして見えますが、やってることはシンプルにただの四則演算です。
コードはこちら。
今回のコードでは、グラフのレンジ(=GraphRange)と総回転数(=loop)は変数で自由に与えられるように作成しています。
# 取得データの変換(pix->G数、pix->差玉)
MaxY = loc[0] # グラフ範囲の上端
MinY = loc[0] + h # グラフ範囲の下端
MinX = min(peakx) # データ範囲の左端
Datapt = len(peakx) # 取得したピークのデータ数
for i in range(len(peakx)):
# データの左端からのピクセル数からG数に変換
peakx[i] = loop / Datapt * (peakx[i] - MinX)
# グラフの上端下端から差玉数に変換
peaky[i] = (((MaxY + MinY) / 2) - peaky[i]) / (MinY - MaxY) * (GraphRange * 2)
・スランプグラフを通常時とRUSH中に分類
次に、取得したデータを通常時とRUSH中に分類します。
今回はシンプルに以下のルールで通常時とRUSH中を判断しています。
もっと賢いルールを作成すると千円Sの計算精度は向上すると思いますが、とりあえずはこんなもんで十分だと思います。
(例えば、インデックスのように遊タイムがロング時短の場合にどうするか等のルール)
1. 今回の差玉が前回の差玉より大きい=RUSH中
2. 今回の差玉が前回の差玉より小さい=通常時
3. 今回の差玉と前回の差玉が同じ=前回の状態を引き継ぐ
コードはこちら。
取得データの先頭には自分より前のデータがないので、強制的に通常時としています。
# 取得データから通常時部分だけを抜き出す
flag = [] # 通常=1、RUSH=0としてフラグを立てていく
i = 0
while i < len(peakx):
# データの開始部分と末尾部分は通常時として扱う
if i == 0:
flag.append(1)
# 開始部分と末尾部分以外は、条件分岐で状態判定する
else:
# 今回の差玉が前回の差玉より大きい場合はRUSH中と判定
if peaky[i] > peaky[i-1]:
flag.append(0)
# 今回の差玉が前回の差玉より小さい場合は通常時と判定
elif peaky[i] < peaky[i - 1]:
flag.append(1)
# 今回の差玉と前回の差玉が同じ場合は、前回の状態を引き継ぐ
elif peaky[i] == peaky[i - 1]:
flag.append(flag[-1])
i = i + 1
# ピーク位置を記録した配列とフラグを入れた配列をまとめる
peak = np.stack([peakx, peaky, flag])
・抽出した通常時部分から千円Sを算出
ようやく最後の項目まで到達しました。
一旦状況を整理すると、配列peakの中はこのように、ゲーム数、差玉、通常時orRUSH中のフラグが入っています。
つまり、配列からフラグが1(=通常時)のデータだけ抽出することで、下図のように通常時部分だけのデータを取得できます。
ここから一本の長い通常時に合成していきますが、シンプルに前のデータとの差分を足していけばOKです。
コードとしては、以下の通りとなります。
通常時のゲーム数と差玉を格納する配列を準備して、上記計算式で値を格納しています。
# 千円スタートを算出する
i = 1
base = [] # 通常時の差玉数を入れる箱
game = [] # 通常時のゲーム数を入れる箱
# 通常時(フラグが1)のデータだけ使用する
while i < len(peak[0][:]):
if peak[2][i] == 1:
# 差玉数とゲーム数の初期値はそのまま入力
if len(base) == 0:
base.append(peak[1][i])
game.append(peak[0][i])
# 初期値以外は、前回データからの差分を入力
else:
base.append(peak[1][i] - peak[1][i-1] + base[-1])
game.append(game[-1] + peak[0][i] - peak[0][i-1])
i = i + 1
最後に、このまま千円Sを算出しても良いですが、下図のように通常時と誤認識した部分がある場合があります。
そこで全体の傾向だけを抽出するために、線形近似を行った上で千円Sを算出すれば、今回の目的は達成です。
# 通常のゲーム数vs差玉数を一次近似
fitting = np.polyfit(game, base, 1)
# 近似式から近似線を計算
fittingline = np.poly1d(fitting)(game)
# 近似式の傾きから250玉当りの回転数=千円スタートを計算
sstart = abs(round(250 / fitting[0], 1))
5. 今回作成したコード
今回作成したコードはこちら。
スランプグラフのタイトルに千円Sの設定値と推測値が表示されるようにしています。
# coding: UTF-8
# 乱数作成用
import random
# ボーダー算出用
import numpy as np
# スランプグラフ描画用
import pylab
# 画像処理用
import cv2
from PIL import Image, ImageOps
# 千円スタート算出用データの作成----ここから----
# 試行回数(RUSH中を含めた総回転数)
loop = 300
# 千円スタートの設定値
回転数 = 18
# グラフのレンジ
GraphRange = 5000
# 大当たり確率の設定
通常時9R時短 = 65536 / 1.000
通常時3R時短 = 129.77 / 0.50
通常時3R通常 = 129.77 / 0.50
時短時9RBonus = 2.15 / 0.10
時短時3RBonus = 2.15 / 0.90
# 乱数範囲の設定準備
通常時9R時短範囲 = round(65536 / 通常時9R時短)
通常時3R時短範囲 = round(65536 / 通常時3R時短)
通常時3R通常範囲 = round(65536 / 通常時3R通常)
時短時9RBonus範囲 = round(65536 / 時短時9RBonus)
時短時3RBonus範囲 = round(65536 / 時短時3RBonus)
# 乱数範囲の設定(通常時)
通常時9R時短範囲_下 = 1
通常時9R時短範囲_上 = 通常時9R時短範囲_下 + 通常時9R時短範囲 - 1
通常時3R時短範囲_下 = 通常時9R時短範囲_上 + 1
通常時3R時短範囲_上 = 通常時3R時短範囲_下 + 通常時3R時短範囲 - 1
通常時3R通常範囲_下 = 通常時3R時短範囲_上 + 1
通常時3R通常範囲_上 = 通常時3R通常範囲_下 + 通常時3R通常範囲 - 1
# 乱数範囲の設定(時短時)
時短時9RBonus範囲_下 = 1
時短時9RBonus範囲_上 = 時短時9RBonus範囲_下 + 時短時9RBonus範囲 - 1
時短時3RBonus範囲_下 = 時短時9RBonus範囲_上 + 1
時短時3RBonus範囲_上 = 時短時3RBonus範囲_下 + 時短時3RBonus範囲 - 1
# 結果用の箱の準備
Result = [] # 差玉数を入れていく
invest = 0 # 使った玉数を入れる
gamecount = 0 # 通常時のゲーム数を入れる(結果の確認用)
# 出玉を入れる箱を0にする
Total = 0
#ループ処理
i = 0
while i <= loop:
i = i + 1
gamecount = gamecount + 1
# 1回転に必要な玉数を減算。
Border = round(np.random.normal(回転数, 2),0)
invest = invest + 250 / Border
Total = Total - (250 / Border)
# 乱数の取得
rand = random.randint(1,65536)
# 当否判定処理
# 時短付きの当りの場合
if 通常時9R時短範囲_下 <= rand <= 通常時3R時短範囲_上:
# 9Rなら9R分の出玉を追加
if 通常時9R時短範囲_下 <= rand <= 通常時9R時短範囲_上:
Total = Total + 720 - 10 * 9
# 3Rなら3R分の出玉を追加
elif 通常時3R時短範囲_下 <= rand <= 通常時3R時短範囲_上:
Total = Total + 240 - 10 * 3
Result.append(Total)
# RUSHに突入させる
j = 0 # 連続外れ回数
# 4連続でハズレるまで計測
while j < 4:
i = i + 1
rand2 = random.randint(1,65536)
# count2 = count2 + 1
# 9Rなら9R分の出玉を追加
if 時短時9RBonus範囲_下 <= rand2 <= 時短時9RBonus範囲_上:
Total = Total + 720 - 10 * 9
j = 0
# 3Rなら3R分の出玉を追加
elif 時短時3RBonus範囲_下 <= rand2 <= 時短時3RBonus範囲_上:
Total = Total + 240 - 10 * 3
j = 0
# ハズレなら連続ハズレ回数を1増やす
else:
j = j + 1
Result.append(Total)
if i == loop:
break
# 通常当りの場合
elif 通常時3R通常範囲_下 <= rand <= 通常時3R通常範囲_上:
Total = Total + 240 - 10 * 3
Result.append(Total)
# はずれの場合
else:
Result.append(Total)
# 結果の表示
pylab.ylim([GraphRange * -1, GraphRange])
pylab.tick_params(direction="in")
pylab.plot(Result)
pylab.savefig("D:\Test\slump.png")
# 千円スタート算出用データの作成----ここまで----
# 千円スタート算出----ここから----
# ターゲット画像の準備
target = cv2.imread(r"D:\Test\slump.png")
target_gray = cv2.cvtColor(target, cv2.COLOR_BGR2GRAY)
cv2.imwrite(r"D:\Test\target_gray.png", target_gray)
# テンプレート画像の準備
template = cv2.imread(r"D:\Test\template.png")
template_gray = cv2.cvtColor(template, cv2.COLOR_BGR2GRAY)
cv2.imwrite(r"D:\Test\template_gray.png", template_gray)
# テンプレートマッチング
match = cv2.matchTemplate(target_gray, template_gray, cv2.TM_CCOEFF_NORMED)
# 類似度が最大値の場所をグラフの位置に決定
loc = np.unravel_index(np.argmax(match), match.shape)
# テンプレート画像をマッチングした位置に移動
# 無地の画像を作成して、そこにテンプレート画像を貼り付ける。
# OpenCVとPillowで画像の読み込みが異なるので、Image.openとcv2.imreadを使って何度も画像を読み込んでいる。
w_tgt, h_tgt = target_gray.shape
ImgMove = Image.new("RGB", (h_tgt, w_tgt), (0, 0, 0))
NumImg_pil = Image.open(r"D:\Test\template_gray.png")
ImgMove.paste(NumImg_pil, (loc[1], loc[0]))
ImgMove.save(r"D:\Test\template_move.bmp")
MoveImg = cv2.imread(r"D:\Test\template_move.bmp", 0)
# モルフォロジを行って微妙な位置ずれでも邪魔なピクセルを消せるようにする。
# 今回はグラフが黒線なのでErosion(収縮)を使う。グラフが白線の場合はDilation(膨張)を使う。
kernel = np.ones((5, 5), np.uint8)
DilImg = cv2.erode(MoveImg, kernel, iterations = 3)
cv2.imwrite(r"D:\Test\target_mor.png", DilImg)
# ターゲット画像を引き算
SubImg = np.where(target_gray < DilImg, target_gray, 0)
cv2.imwrite(r"D:\Test\target_sub.png", SubImg)
# 画像の走査
peakx = []
peaky = []
# テンプレート画像のサイズ
w, h = template_gray.shape[::-1]
# 画像の走査範囲の描画
cv2.rectangle(target, (loc[1], loc[0]), (loc[1] + w, loc[0] + h), (0, 0, 255), 2)
cv2.imwrite(r"D:\Test\target_match.png", target)
# ピーク位置(スランプグラフ)の検出
for i in range(loc[1], loc[1] + w):
for j in range(loc[0], loc[0] + h):
# ピーク位置(画素が白=255のところがグラフの位置)
if SubImg[j, i] != 0:
peakx.append(i)
peaky.append(j)
# X方向1pixごとに、Y方向のピークは1個見つかればOK
break
# 画像内のピーク位置(スランプグラフ位置)に青点を描画
for i in range(len(peakx)):
cv2.rectangle(target, (peakx[i] - 1, peaky[i] - 1), (peakx[i] + 1, peaky[i] + 1), (255,0,), 2)
cv2.imwrite(r"D:\Test\target_peak.png", target)
# 取得データの変換(pix->G数、pix->差玉)
MaxY = loc[0] # グラフ範囲の上端
MinY = loc[0] + h # グラフ範囲の下端
MinX = min(peakx) # データ範囲の左端
Datapt = len(peakx) # 取得したピークのデータ数
for i in range(len(peakx)):
# データの左端からのピクセル数からG数に変換
peakx[i] = loop / Datapt * (peakx[i] - MinX)
# グラフの上端下端から差玉数に変換
peaky[i] = (((MaxY + MinY) / 2) - peaky[i]) / (MinY - MaxY) * (GraphRange * 2)
# 取得データから通常時部分だけを抜き出す
flag = [] # 通常=1、RUSH=0としてフラグを立てていく
i = 0
while i < len(peakx):
# データの開始部分と末尾部分は通常時として扱う
if i == 0:
flag.append(1)
# 開始部分と末尾部分以外は、条件分岐で状態判定する
else:
# 今回の差玉が前回の差玉より大きい場合はRUSH中と判定
if peaky[i] > peaky[i-1]:
flag.append(0)
# 今回の差玉が前回の差玉より小さい場合は通常時と判定
elif peaky[i] < peaky[i - 1]:
flag.append(1)
# 今回の差玉と前回の差玉が同じ場合は、前回の状態を引き継ぐ
elif peaky[i] == peaky[i - 1]:
flag.append(flag[-1])
i = i + 1
# ピーク位置を記録した配列とフラグを入れた配列をまとめる
peak = np.stack([peakx, peaky, flag])
# 千円スタートを算出する
i = 1
base = [] # 通常時の差玉数を入れる箱
game = [] # 通常時のゲーム数を入れる箱
# 通常時(フラグが1)のデータだけ使用する
while i < len(peak[0][:]):
if peak[2][i] == 1:
# 差玉数とゲーム数の初期値はそのまま入力
if len(base) == 0:
base.append(peak[1][i])
game.append(peak[0][i])
# 初期値以外は、前回データからの差分を入力
else:
base.append(peak[1][i] - peak[1][i-1] + base[-1])
game.append(game[-1] + peak[0][i] - peak[0][i-1])
i = i + 1
# 通常のゲーム数vs差玉数を一次近似
fitting = np.polyfit(game, base, 1)
# 近似式から近似線を計算
fittingline = np.poly1d(fitting)(game)
# 近似式の傾きから250玉当りの回転数=千円スタートを計算
sstart = abs(round(250 / fitting[0], 1))
# データの出力
pylab.title("設定:" + str(round((gamecount / invest * 250), 1)) + "[回/k], 推測:" + str(sstart) + "[回/k]", fontname="MS Gothic")
pylab.xlabel("総回転数[回]", fontname="MS Gothic")
pylab.ylabel("差玉[玉]", fontname="MS Gothic")
pylab.savefig("D:\Test\slump_tracer.png")
pylab.show()
# 千円スタート算出----ここまで----
6. 結果の確認
早速、何回かテストを行って千円Sの算出が正常に行われているか確認していきます。
テスト1:通常時だけのスランプグラフ
まずは、通常時だけのスランプグラフから。
ここができていないと今までの苦労が水の泡ですが、結果はこちら!
設定値と推測値がともに17.7[回/k]ということで完璧ですね。
テスト2:RUSHに入った時のスランプグラフ
続いてこちら。RUSHに入った時のスランプグラフです。
RUSH中を良い感じに判断できていれば問題ないはずですが、結果はこちら!
設定値が17.7[回/k]に対して、推測値が17.5[回/k]ということでまあまあ許容範囲内の誤差で収まっていると思います。
テスト3:チョロ出玉の時のスランプグラフ
続いてこちら。チョロ出玉の時のスランプグラフです。
チョロ出玉部分はスランプグラフの変化があまりないのでやや不安ですが、結果はこちら!
設定値が17.8[回/k]に対して、推測値が17.5[回/k]ということでほぼテスト2のRUSH時と同レベルの算出精度が出せています。
テスト4:グラフが上限突破したときのスランプグラフ
最後のテストはこちら。たまに見かけますが、スランプグラフがグラフの上限から飛び出てしまうパターンですね。
結果はこちら!
設定値が17.7[回/k]に対して、推測値が33.8[回/k]ということで全然ダメですね。
当然と言えば当然ですが、上限突破するとスランプグラフを追跡できないので、仕方ない部分ではあります。
ただ、ログデータを見る限り上限突破するまでのスランプグラフはちゃんと追跡できているので、上限突破したG数がわかれば他のテストと同レベルの算出精度は出せると思います。
ということで、スランプグラフから千円Sを算出する方法をプログラミングしてみました。
比較的精度よく算出できていると思うので、データサイトで打つ台を選ぶ際の指針の一つにはできそうです。























大変参考になる記事をお書き下さり、ありがとうございます。
返信削除もしよろしければ、以下の点について質問させて頂きたく思います。
「回転ムラの考慮方法」の部分に、random.normal関数の基準として18という値を用いたと記載してありますが、なぜこの値を用いたのでしょうか。素人ながら、この値次第で千円Sが変化するのではないかと感じました。
ご覧いただきありがとうございます。
削除せっかくご質問いただいたのにお返事が遅くなり、申し訳ございません。
結論から言うと、18という値に理由はありません。
お察しの通り、この値次第で千円Sが変化します。
つまり、「random.normal関数の基準として18という値を用いた」=「千円18回転回るパチンコ台を用意した。」というイメージです。
強いて言えば、「例えば千円100回転回るパチンコ台を用意してシミュレーションしても現実離れしていて意味がないので、それらしい値として18を採用しました。」くらいです。