P牙狼MAXXのシミュレーション
お世話になっております、スログラミングです。
牙狼の新台が出るらしいですね。
Rush中は10Roundが81%でループするようで、初代が好きだった私としては非常に楽しみです。
(初代を打ったことがあると言うとある程度年齢がバレそうですが、、)
ホール導入は4月頃?という情報も見かけましたが、一足先にどんなスランプグラフになりそうかシミュレーションしてみたいと思います。
では早速Pythonでコーディングしていきましょう。
※中身の数値等はスログラミング調べなので、実機とは異なる可能性があります。
今回のアジェンダはこちら。
1. 遊タイムのコーディング
2. 今回作成したコード
3. 結果の確認

にほんブログ村
2. 今回作成したコード
3. 結果の確認
1. 遊タイムのコーディング
牙狼MAXXは1種2種混合機だと言われています。
1種2種混合機の遊タイムといえば、Pモモキュンソード等をイメージしてもらえるとわかるように、遊タイム突入=RUSHとなります。
以前遊タイムのプログラミングを行ったPとある魔術の禁書目録(インデックス)はST機だったので、遊タイム=ただの時短でしたね。
細かくは理解していないので説明できませんが、シミュレーション上は1種2種の遊タイムはRUSHの数値で計算とだけ覚えておけばOKです。
(小当たりが~とか、確率変動の契機は~とか色々細かい話があるみたいです。)
1.1. フローチャート
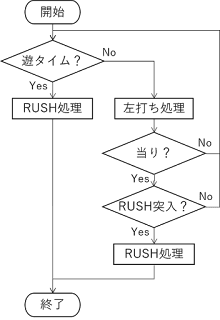
今回はこのようなフローチャートでプログラミングを行っていきます。
いきなり遊タイム中か否かの判定を行った上で、遊タイム中ならRUSHの処理、遊タイム中以外であれば通常時の処理を行います。
RUSH中の処理が2箇所あるのがちょっとかっこ悪いですが、良い方法が思い浮かばなかったのでご容赦ください。
ざっくりとしたプログラムはこのような感じです。
いつものようにfor分で1回転ごとの処理を行いつつ、遊タイム中とそれ以外の判定を行った上で中身の処理を記載しています。
"Total"という変数に現在の差玉数を入力していきます。
#ループ処理(loopで設定した回数だけシミュレーションを行う。)
for i in range(loop):
# 250発あたりの回転数から、1回転に必要な玉数を算出して減算
Total = Total - (250 / Border)
# 乱数の取得
rand = random.randint(1,65536)
# 遊タイムの処理
# 951回転から遊タイム突入。
if 950 < ゲーム数 < 951 + 200:
# RUSH中の処理を記載
# 遊タイム以外の処理
else:
# 通常時の処理を記載
1.2. 遊タイムの中身のコード
遊タイムの中身の部分は以下のようなコードでシミュレートしています。
前述した通り、この部分はRUSH中の処理と同じです。
今出回っている情報では、右打ち中の当りは81%がRUSH(時短)付き、残りの19%がRUSH(時短)無し、ということなので、RUSH無の大当たりを引いたときには"break"でRUSH中の処理から抜けるようにしています。
# Rush回数までループする処理
while ゲーム数_Rush <= 200:
# Rush中の1回転に必要な玉数を算出して減算
Total = Total - (250 / Border_Rush)
# 乱数の取得
rand2 = random.randint(1,65536)
# Rush付き10Rの振り分けだったとき
if 右10RRush範囲_下 <= rand2 <= 右10RRush範囲_上:
Total = Total + 1500 - 10 * 10
ゲーム数_Rush = 1
# 10R通常の振り分けだったとき
elif 右10R通常範囲_下 <= rand2 <= 右10R通常範囲_上:
Total = Total + 1500 - 10 * 10
ゲーム数_Rush = 1
# Rushを抜ける
break
# はずれのとき
else:
ゲーム数_Rush = ゲーム数_Rush + 1
2. 今回作成したコード
最終的には以下のようなコードを作成しました。
いつものようにグラフ表示を行っていますが、遊タイム期間だけグラフの背景の色を変更しています。
# coding: UTF-8
# 乱数作成用
import random
# スランプグラフ描画用
import matplotlib.pyplot as plt
import pylab
# 試行回数
loop = 1000000
# 1k(250玉)あたりの回転数(左打ち)
Border = 17.5
# 1k(250玉)打って何発残るか(右打ち)。今回は10%減→90%残る仮定で計算
Border_Rush = 250 * 0.90
# 大当たり確率の設定(左打ち)
左3RRush = 319.7 / 0.50
左3R通常 = 319.7 / 0.50
# 乱数範囲の設定準備(左打ち)
左3RRush範囲 = round(65536 / 左3RRush)
左3R通常範囲 = round(65536 / 左3R通常)
# 乱数範囲の設定(左打ち)
左3RRush範囲_下 = 1
左3RRush範囲_上 = 左3RRush範囲_下 + 左3RRush範囲 - 1
左3R通常範囲_下 = 左3RRush範囲_上 + 1
左3R通常範囲_上 = 左3R通常範囲_下 + 左3R通常範囲 - 1
# 大当たり確率の設定(右打ち)
右10RRush = 1.08 / 0.81
右10R通常 = 1.08 / 0.19
# 乱数範囲の設定準備(右打ち)
右10RRush範囲 = round(65536 / 右10RRush)
右10R通常範囲 = round(65536 / 右10R通常)
# 乱数範囲の設定(右打ち)
右10RRush範囲_下 = 1
右10RRush範囲_上 = 右10RRush範囲_下 + 右10RRush範囲 - 1
右10R通常範囲_下 = 右10RRush範囲_上 + 1
右10R通常範囲_上 = 右10R通常範囲_下 + 右10R通常範囲 - 1
# 結果用の箱やカウンタの準備
Result = [] # グラフ描画用に1回転ごとの差玉を入れる
Total = 0 # トータルの差玉を入れる
ゲーム数 = 1 # 前回大当たりからの通常ゲーム数を入れる
ゲーム数_トータル = 1 # Rush中を含めた全てのゲーム数を入れる(グラフ用)
遊タイム中 = [] # グラフで遊タイム中の背景色を変えるための配列(グラフ用)
初当たり回数 = 0 # 初当たり回数のカウント(結果表示用)
#ループ処理(loopで設定した回数だけシミュレーションを行う。)
for i in range(loop):
# 250発あたりの回転数から、1回転に必要な玉数を算出して減算
Total = Total - (250 / Border)
# 乱数の取得
rand = random.randint(1,65536)
# 遊タイムの処理
# 951回転から遊タイム突入。
if 950 < ゲーム数 < 951 + 200:
# 遊タイム期間の保存(グラフ用)
遊タイム中.append(ゲーム数_トータル)
print(ゲーム数, "遊タイム")
# Rush中のゲーム数をカウント
ゲーム数_Rush = 1
# Rush回数までループする処理
while ゲーム数_Rush <= 200:
# Rush中の1回転に必要な玉数を算出して減算
Total = Total - (250 / Border_Rush)
# 乱数の取得
rand2 = random.randint(1,65536)
# Rush付き10Rの振り分けだったとき
if 右10RRush範囲_下 <= rand2 <= 右10RRush範囲_上:
Total = Total + 1500 - 10 * 10
print("-", ゲーム数_Rush, "10RRush")
ゲーム数_Rush = 1
# 大当たりしたのでゲーム数を0に戻す
ゲーム数 = 0
# 10R通常の振り分けだったとき
elif 右10R通常範囲_下 <= rand2 <= 右10R通常範囲_上:
Total = Total + 1500 - 10 * 10
print("-", ゲーム数_Rush, "10R通常")
ゲーム数_Rush = 1
# 大当たりしたのでゲーム数を0に戻す
ゲーム数 = 0
# Rushを抜ける
break
# はずれのとき
else:
ゲーム数_Rush = ゲーム数_Rush + 1
Result.append(Total)
# ゲーム数をカウント(グラフ用)
ゲーム数_トータル = ゲーム数_トータル + 1
# 遊タイム期間の保存(グラフ用)
遊タイム中.append(ゲーム数_トータル)
# 遊タイム以外の処理
else:
# 当り判定+連荘処理
# Rush付きの大当たりを引いた時の処理
if 左3RRush範囲_下 <= rand <= 左3RRush範囲_上:
# 大当たりで獲得した玉数を加算(アタッカーに入れた玉数は減算する)
Total = Total + 450 - 3 * 10
# 当たった時のゲーム数を表示
print(ゲーム数, "左3RRush")
# 初当たり回数のカウント
初当たり回数 = 初当たり回数 + 1
Result.append(Total)
# 大当たりしたのでゲーム数を0に戻す
ゲーム数 = 0
# Rush中の処理
# Rush中のゲーム数をカウント
ゲーム数_Rush = 1
# Rush回数までループする処理
while ゲーム数_Rush <= 200:
# Rush中の1回転に必要な玉数を算出して減算
Total = Total - (250 / Border_Rush)
# 乱数の取得
rand2 = random.randint(1,65536)
# Rush付き10Rの振り分けだったとき
if 右10RRush範囲_下 <= rand2 <= 右10RRush範囲_上:
Total = Total + 1500 - 10 * 10
print("-", ゲーム数_Rush, "10RRush")
ゲーム数_Rush = 1
# 10R通常の振り分けだったとき
elif 右10R通常範囲_下 <= rand2 <= 右10R通常範囲_上:
Total = Total + 1500 - 10 * 10
print("-", ゲーム数_Rush, "10R通常")
ゲーム数_Rush = 1
# Rushを抜ける
break
# はずれのとき
else:
ゲーム数_Rush = ゲーム数_Rush + 1
Result.append(Total)
# ゲーム数をカウント(グラフ用)
ゲーム数_トータル = ゲーム数_トータル + 1
# 通常当たりを引いた時の処理
elif 左3R通常範囲_下 <= rand <= 左3R通常範囲_上:
# 大当たりで獲得した玉数を加算(アタッカーに入れた玉数は減算する)
Total = Total + 450 - 3 * 10
# 当たった時のゲーム数を表示
print(ゲーム数, "左3R通常")
# 初当たり回数のカウント
初当たり回数 = 初当たり回数 + 1
Result.append(Total)
# 大当たりしたのでゲーム数を0に戻す
ゲーム数 = 0
else:
# はずれたときの処理
# 玉数をそのまま配列に格納
Result.append(Total)
# 前回大当たりからのゲーム数をカウント
ゲーム数 = ゲーム数 + 1
# ゲーム数をカウント(グラフ用)
ゲーム数_トータル = ゲーム数_トータル + 1
# 結果の表示
pylab.plot(Result)
# 遊タイム中はグラフの背景の色を変える
イテレータ = iter(遊タイム中)
for start, end in zip(イテレータ, イテレータ):
pylab.axvspan(start, end, color="magenta", alpha=0.3)
print("初当たり確率:", round(loop / 初当たり回数, 0), "(初当たり:", 初当たり回数, "回)")
print("玉数:", round(Total, 0), "(玉)")
pylab.show()
plt.show()
3. 結果の確認
せっかくシミュレータを作成したので、ボーダーがどのくらいになるのかを確認してみます。
1k(250玉)あたりの回転数を変更しながら、通常時を1000万回転回したときの結果はこのようになりました。
(遊タイム中のピンクじゃまですね。すみません。。)
1kあたりの回転数を17, 17.5, 18と振っていますが、1kあたり18回転回るとプラスになりそうです。
ということで、P牙狼MAXXのシミュレータを作成してみました。
ボーダー的にはいわゆる甘い(スペックが良い)台になりそうなので、一度は良い思いができることを期待してます。
にほんブログ村

コメント
コメントを投稿