P大工の源さん 超韋駄天 VS P牙狼MAXX VS ぱちんこ ウルトラマンタロウ2
お世話になっております、スログラミングです。
ちょっと本業が忙しくてバタバタしている間に牙狼MAXXより凄そうな機種が出てきましたね。
その名も「ぱちんこ ウルトラマンタロウ2」。
ネットに出回っているスペック情報を見る限り夢のありそうな機種で、導入を楽しみにしてます。
最近は閉店間際の最後の勝負で韋駄天に座ることが多いですが、これからは牙狼MAXXやタロウ等も選択肢に入ってくると思います。
ということで来るべき日に備えて、「P大工の源さん 超韋駄天」「P牙狼MAXX」「ぱちんこ ウルトラマンタロウ2」のRUSH性能を比較して、どれを打つか比較してみたいと思います。
(以下、機種名称は適当に略します。)
では早速Pythonでコーディングしていきましょう。
※中身の数値等はスログラミング調べなので、実機とは異なる可能性があります。
※また、今回右打ち中の玉減り等は無視しています。
今回のアジェンダはこちら。
1. タロウのRUSH処理作成
2. 3者の比較方法
3. 今回作成したコード
4. 結果の確認

にほんブログ村
2. 3者の比較方法
3. 今回作成したコード
4. 結果の確認
1. タロウのRUSH処理作成
まず、タロウのRUSH処理を作成していきます。
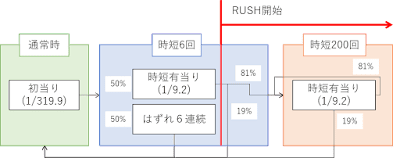
タロウのゲームフローは以下のような形となっています。
意外と複雑ですが、ざっくりいうと、初当りの50%でRUSH突入、その内20%はRUSH即終了ってことですね。
どこをRUSH開始と置くかで今回のシミュレーションの結果が多少変わってきますが、今回は図に記載した位置をRUSH開始としています。
タロウのRUSH処理は以下のコードとしました。
厳密には今回想定したRUSH開始位置だと、初回のみ当りが確定した状態でスタートしますが、結果に影響はないので牙狼のコードを使いまわしています。
(プログラミングしながら思いましたが、"GARO"と"TARO"って一文字違いですね。)
(まさか発売前からライバルとして意識して開発してたのか。)
ゲーム数 = 1
# タロウのRUSH処理
while ゲーム数 <= 900:
# 乱数の取得
rand = random.randint(1,65536)
# Rush付き10Rの振り分けだったとき
if 右10RRush範囲_下_taro <= rand <= 右10RRush範囲_上_taro:
Total_taro = Total_taro + 1600 - 10 * 10
ゲーム数 = 1
# 10R通常の振り分けだったとき
elif 右10R通常範囲_下_taro <= rand <= 右10R通常範囲_上_taro:
Total_taro = Total_taro + 1600 - 10 * 10
ゲーム数 = 1
# Rushを抜ける
break
# はずれのとき
else:
ゲーム数 = ゲーム数 + 1
2. 3機種の比較方法
これで、3機種分のRUSH処理が完成したので、どうやって対決していくかを記載していきます。
トーナメント戦やリーグ戦等色々考えてみましたが、ここはシンプルに以下の図に示す方法で比較してみます。
ざっくりいうと、RUSH1回毎に3機種の出玉を比較→1位の機種を勝者と判定→10000回ループです。
比較部分のコードはこんな感じです。
ちょっとかっこ悪いですが、書きやすさ重視でif文をひたすら使ってます。
# RUSH毎に出玉数が多かった方の機種名を入れる
if Total_idaten > Total_garo and Total_idaten > Total_taro:
Result.append("Idaten")
elif Total_garo > Total_idaten and Total_garo > Total_taro:
Result.append("Garo")
elif Total_taro > Total_idaten and Total_taro > Total_garo:
Result.append("Taro")
else:
Result.append("Even")
3. 今回作成したコード
最終的には以下のようなコードを作成しました。
せっかくなので出玉分布のヒストグラムと統計値も出力しています。
# coding: UTF-8
# 乱数作成用
import random
# グラフ描画用
import pylab
# 統計値取得用
import statistics
# 試行回数
loop = 10000
# RUSH中の確率の設定(韋駄天)
時短時9RBonus = 2.06 / 0.20
時短時3RBonus = 2.06 / 0.80
# 乱数範囲の設定準備(韋駄天)
時短時9RBonus範囲 = round(65536 / 時短時9RBonus)
時短時3RBonus範囲 = round(65536 / 時短時3RBonus)
# 乱数範囲の設定(韋駄天)
時短時9RBonus範囲_下 = 1
時短時9RBonus範囲_上 = 時短時9RBonus範囲_下 + 時短時9RBonus範囲 - 1
時短時3RBonus範囲_下 = 時短時9RBonus範囲_上 + 1
時短時3RBonus範囲_上 = 時短時3RBonus範囲_下 + 時短時3RBonus範囲 - 1
# RUSH中の確率の設定(牙狼)
右10RRush = 1.08 / 0.81
右10R通常 = 1.08 / 0.19
# 乱数範囲の設定準備(牙狼)
右10RRush範囲 = round(65536 / 右10RRush)
右10R通常範囲 = round(65536 / 右10R通常)
# 乱数範囲の設定(牙狼)
右10RRush範囲_下 = 1
右10RRush範囲_上 = 右10RRush範囲_下 + 右10RRush範囲 - 1
右10R通常範囲_下 = 右10RRush範囲_上 + 1
右10R通常範囲_上 = 右10R通常範囲_下 + 右10R通常範囲 - 1
# RUSH中の確率の設定(タロウ)
右10RRush_taro = 9.20 / 0.81
右10R通常_taro = 9.20 / 0.19
# 乱数範囲の設定準備(タロウ)
右10RRush範囲_taro = round(65536 / 右10RRush_taro)
右10R通常範囲_taro = round(65536 / 右10R通常_taro)
# 乱数範囲の設定(タロウ)
右10RRush範囲_下_taro = 1
右10RRush範囲_上_taro = 右10RRush範囲_下_taro + 右10RRush範囲_taro - 1
右10R通常範囲_下_taro = 右10RRush範囲_上_taro + 1
右10R通常範囲_上_taro = 右10R通常範囲_下_taro + 右10R通常範囲_taro - 1
# 結果集計用の箱の準備
Result = [] # RUSH毎に獲得数が多かった方の機種名を入れる
Result_idaten = [] # RUSH毎の獲得玉数を入れる(韋駄天用)
Result_garo = [] # RUSH毎の獲得玉数を入れる(牙狼用)
Result_taro = [] # RUSH毎の獲得玉数を入れる(タロウ用)
#ループ処理(loopで設定した回数だけシミュレーションを行う。)
for i in range(loop):
# Rush中のゲーム数をカウント
ゲーム数 = 1
# Rush中の獲得玉数をリセット(初当りの玉数を入れておく)
Total_idaten = 660 - 10 * 6 # トータルの差玉を入れる(韋駄天用)
Total_garo = 450 - 10 * 3 # トータルの差玉を入れる(牙狼用)
Total_taro = 300 - 10 * 2 # トータルの差玉を入れる(タロウ用)
# 韋駄天のRUSH処理
while ゲーム数 < 5:
# 乱数の取得
rand = random.randint(1, 65536)
# 9Rの振り分けだったとき
if 時短時9RBonus範囲_下 <= rand <= 時短時9RBonus範囲_上:
Total_idaten = Total_idaten + 990 - 10 * 9
ゲーム数 = 1
# 3Rの振り分けだったとき
elif 時短時3RBonus範囲_下 <= rand <= 時短時3RBonus範囲_上:
Total_idaten = Total_idaten + 330 - 10 * 3
ゲーム数 = 1
# はずれのとき
else:
ゲーム数 = ゲーム数 + 1
# 韋駄天のRUSH後の獲得玉数を入れる
Result_idaten.append(Total_idaten)
ゲーム数 = 1
# 牙狼のRUSH処理
while ゲーム数 <= 200:
# 乱数の取得
rand = random.randint(1,65536)
# Rush付き10Rの振り分けだったとき
if 右10RRush範囲_下 <= rand <= 右10RRush範囲_上:
Total_garo = Total_garo + 1500 - 10 * 10
ゲーム数 = 1
# 10R通常の振り分けだったとき
elif 右10R通常範囲_下 <= rand <= 右10R通常範囲_上:
Total_garo = Total_garo + 1500 - 10 * 10
ゲーム数 = 1
# Rushを抜ける
break
# はずれのとき
else:
ゲーム数 = ゲーム数 + 1
# 牙狼のRUSH後の獲得玉数を入れる
Result_garo.append(Total_garo)
ゲーム数 = 1
# タロウのRUSH処理
while ゲーム数 <= 900:
# 乱数の取得
rand = random.randint(1,65536)
# Rush付き10Rの振り分けだったとき
if 右10RRush範囲_下_taro <= rand <= 右10RRush範囲_上_taro:
Total_taro = Total_taro + 1600 - 10 * 10
ゲーム数 = 1
# 10R通常の振り分けだったとき
elif 右10R通常範囲_下_taro <= rand <= 右10R通常範囲_上_taro:
Total_taro = Total_taro + 1600 - 10 * 10
ゲーム数 = 1
# Rushを抜ける
break
# はずれのとき
else:
ゲーム数 = ゲーム数 + 1
# 牙狼のRUSH後の獲得玉数を入れる
Result_taro.append(Total_taro)
ゲーム数 = 1
# RUSH毎に出玉数が多かった方の機種名を入れる
if Total_idaten > Total_garo and Total_idaten > Total_taro:
Result.append("Idaten")
elif Total_garo > Total_idaten and Total_garo > Total_taro:
Result.append("Garo")
elif Total_taro > Total_idaten and Total_taro > Total_garo:
Result.append("Taro")
else:
Result.append("Even")
# RUSH毎の獲得玉数の表示
print("韋駄天:", Total_idaten, "(玉)", "牙狼:", Total_garo, "(玉)", "タロウ:", Total_taro, "(玉)")
# 結果の表示
print("--------------------")
print("韋駄天:", sum([x.endswith('Idaten') for x in Result]), "勝, ", "牙狼:", sum([x.endswith('Garo') for x in Result]), "勝", "タロウ:", sum([x.endswith('Taro') for x in Result]), "勝")
print("平均値・・・", "韋駄天:", statistics.mean(Result_idaten), "(玉), ", "牙狼:", statistics.mean(Result_garo), "(玉)", "タロウ:", statistics.mean(Result_taro), "(玉)")
print("中央値・・・", "韋駄天:", statistics.median(Result_idaten), "(玉), ", "牙狼:", statistics.median(Result_garo), "(玉)", "タロウ:", statistics.median(Result_taro), "(玉)")
print("3Sigma・・・", "韋駄天:", round(3 * statistics.stdev(Result_idaten), 0), "(玉), ", "牙狼:", round(3 * statistics.stdev(Result_garo), 0), "(玉)", "タロウ:", round(3 * statistics.stdev(Result_taro), 0), "(玉)")
print("最大値・・・", "韋駄天:", max(Result_idaten), "(玉), ", "牙狼:", max(Result_garo), "(玉)", "タロウ:", max(Result_taro), "(玉)")
# ヒストグラムの描画
pylab.figure()
hi1 = pylab.hist(Result_idaten, bins=50, color='red', alpha=0.5)
hi2 = pylab.hist(Result_garo, bins=50, color='blue', alpha=0.5)
hi3 = pylab.hist(Result_taro, bins=50, color='green', alpha=0.5)
pylab.legend(["韋駄天", "牙狼", "タロウ"], prop={"family":"MS Gothic"})
pylab.title("韋駄天vs牙狼vsタロウ", fontname="MS Gothic")
pylab.show()
4. 結果の確認
作成したコードを実行した結果はこちら。
見やすくするために、グラフ中の表は人力でエクセルに書き写したものを貼り付けています。
タロウ強いですね。
継続率は、牙狼とほぼ同じなので、タロウチャッカーの威力だと思います。
対して、韋駄天は一番左の1800発以下の頻度が多いところが足を引っ張っていますね。
(やっぱり、牙狼とタロウはRUSHに入りさえすれば1500発とれるのはデカい。)
また、統計値でそんなに気になる数値はないですが、一応簡単なコメントを。
・平均値
全データの合計をデータ数で割ったものです。
簡単に算出できて便利ですが、外れ値の影響を受けやすいです。
例えば、5万発オーバーの剛腕の人がいたりすると、平均値も大きめになってしまいます。
・中央値
全データを上から順番に並べたときに真ん中にある値です。
(全データでなく外れ値を除外することもあります。)
平均値よりも外れ値の影響を受けにくいです。
・3Sigma(3σ)
標準偏差(ばらつき)を3倍したものです。
3倍じゃなく、1倍や2倍したものをσ・2σといいます。
全データの99.7%が平均+3σの範囲に入ります。
(ちなみに、σで68%、2σで95%らしいです。)
値が大きいものほど、波が荒いスペックだと言えます。
逆に平均+3σを超える出玉を獲得した場合は、剛腕を自慢してください。
ということで、韋駄天 vs ガロ vs タロウのRUSH性能を比較してみました。
結果は、韋駄天 < ガロ ≦ タロウとなりました。
とはいえ、韋駄天の突入率60%も魅力的ですし、タロウのヘソ賞球1個は辛そうな気もします。
同じ規則内で作ってるので、出玉設計思想の差とも言えますね。
(ぱちんこ GANTZ極は小当りRUSHに全振りですし。)
ちなみにここまでシミュレーションしておいてなんですが、私はとりあえず全部打ってから決めます。
にほんブログ村



コメント
コメントを投稿